En esta publicación se expondrá un sintético análisis sobre la forma de evaluar las Incertidumbres de medición. En ese sentido, se ha considerado importante tomar de referencia los fundamentos de la Recomendación sobre las Incertidumbres, propuesta oportunamente por el Comité Internacional de Pesas y Medidas, y basada en criterios estadísticos de aplicación, generando un cambio sustancial en el resultado de las mediciones.

Conceptos generales

El objetivo que se plantea generalmente en una Medición, es explicitar la naturaleza particular de la Magnitud sometida a la medición o Mesurando e incursionar sobre la forma de obtener el Valor medido y establecer la expresión de la Incertidumbre asociada, que define el Intervalo de validez del resultado. En consecuencia, siempre el Valor medido será aproximado del Mesurando en cuestión y podrá obtenerse únicamente su valor exacto, a través del Conteo.
Los procedimientos de medición, no son rutinarios ni puramente matemáticos pues exigen un profundo conocimiento sobre la naturaleza de los Mesurandos de la técnica empleada, del instrumental utilizado y de los presuntos efectos Sistemáticos y Aleatorios involucrados en la medición, que deberían ser desafectados o eventualmente reducidos según las condiciones operativas implementadas. Ello implica que en algunos casos se requiera una Valoración sobre la eficacia de la Metodología adoptada, de los Patrones utilizados, y una verificación sobre la Trazabilidad metrológica interna del laboratorio, en el sentido que una eventual comparación con terceros resulte satisfactoria.
Se recuerda que el Comité Internacional de Pesas y Medidas (CIPM), consciente con esta situación, tomó la iniciativa de crear un grupo de trabajo por intermedio de la Oficina Internacional respectiva (OIPM) con el encargo de armonizar el tratamiento de las Incertidumbres experimentales y cuyas conclusiones fueron dadas en la Recomendación INC-1 (1980).
Este documento contiene las bases científicas a seguir en la evaluación de las Incertidumbres, agrupándolas en dos categorías diferentes denominadas Tipos “A” y ”B”, y por lo tanto extendidas a las respectivas mediciones. La novedad fundamental de esta Recomendación, estriba que considera a todas las componentes de Incertidumbres dependientes de Variancias presentes en la medición, es decir como una variable aleatoria para distintas Densidades de probabilidad.
Con posterioridad han aparecido importantes publicaciones basadas en esa Recomendación. En especial la ISO/IEC “Guide to expression uncertainty in measurement” denominada usualmente (GUM), traducida por IRAM en la norma 35050 (2001), y el documento EA 4/02 “Expression of the uncertainty of measurement in calibration” del organismo de Acreditación Europeo traducido en la norma 35051(2004).
Sobre la base de la citada recomendación y a las publicaciones precedentes, se ha considerado razonable interpretar las aludidas incertidumbres en los siguientes términos.

“Tipo A”: Aquellas Incertidumbres que se evalúan por medios estadísticos de carácter objetivo, mediante observaciones repetitivas, y en “iguales condiciones operativas”.

“Tipo B”: Aquellas Incertidumbres que se evalúan por otros medios no repetitivos de carácter subjetivo, basadas en la experiencia, y vinculadas en general a supuestas Distribuciones de probabilidades arbitrarias, con límites conocidos.
Dada la importancia de estas Incertidumbres fueron incorporadas al Vocabulario Internacional de Metrología (VIM) JCGM 200:2008 con los títulos indicados en las siguientes cláusulas:
2.28 “Evaluación tipo A de la Incertidumbre de medición”
2.29“Evaluación tipo B de la Incertidumbre de medición”

Tratamiento específico

A continuación se analizará con cierto detalle el origen y evaluación de las respectivas incertidumbres, basadas sobre aspectos estadísticos, con indicación de valores de referencia y relacionadas a las Mediciones del tipo Directa.#
# Las Mediciones Indirectas serán objeto de otra Publicación

La Incertidumbre tipo “A” u_(A)

Como ya se había definido, estas Incertidumbres derivan del hecho de repetir observaciones en “iguales condiciones operativas”, esta característica particular, no podría ser analizada a partir de la clásica Teoría estadística de Laplace-Gauss por incumplimiento de sus postulados, pero si por similitud de la anterior y con justeza mediante la Teoría de la Distribución de las Muestras de una supuesta Población, y que fuera propuesta por Gosset(Student) y publicada en 1908.

Como hipótesis de trabajo es importante destacar que la distribución de Gosset representa la forma más   realista para la evaluación de la Incertidumbre tipo A, por ello fue adoptada en esta Publicación a ser utilizada con miras al futuro                                                                                                              

En la práctica las condiciones de repetibilidad o “iguales condiciones operativas”, que se impone al procedimiento de medición de una magnitud física, resulta técnicamente complejo. En particular respecto a las magnitudes de influencia actuantes, resulta difícil asegurar su constancia en el tiempo, como así también como otros factores que deben ser mantenidos invariables, durante la medición. Por lo tanto, la cantidad de observaciones en esas condiciones de repetibilidad no resultan  numerosas.

El estudio se encara a partir del análisis de la función de distribución de Gosset, de la cual la variable aleatoria t está estrechamente ligada con la fundamental relación estadística que vincula el apartamiento del Valor medido V respecto al Mesurando µ , referido a la Dispersion S* de la Media aritmética o Valor medido es decir:                                                               

Como elementos de referencia, se introducen los conocidos parámetros de dispersión: el Desvío estándar experimental “s”, caracterizado por una serie de “n” observaciones repetidas previas correcciones sistemáticas, y el Desvío estándar experimental de la Media aritmética “S*” que mide la Dispersión de las Medias de las Muestras, en relación con la supuesta Población.  Estos parámetros estadísticos están vinculados a través de la conocida expresión:

       

De donde: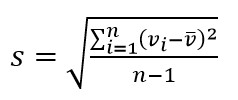              

Se deduce de la expresión estadística anterior, que la diferencia entre el Valor medido y el Mesurando resulta igual al citado parámetro de dispersión S* por la variable t es decir:           

No resulta fácil interpretar la coherencia entre ambos términos igualitarios con identidad en la unidad, sin embargo   tratándose de una consecuencia del   Análisis estadístico es razonable aceptar, que este apartamiento aleatorio resulte incierto por la presencia del Mesurando.

Esta situación como una alternativa de solución, se resuelve asimilando el concepto anterior a través del término (S*.t) , con el nombre moderno de  Incertidumbre de medición, simbolizada u_{(A) ,}que asociada al Valor medido, suministra el Resultado de la medición . Los límites del probable intervalo 2u_(A) definen la zona de pertenencia del Mesurando.

Para una probabilidad de ocurrencia razonable del   68,3% y con las cifras significativas fijadas a la diferencia (n-1), denominada grados de libertad, le corresponde al parámetro   t  los siguientes  valores  estadísticos:

(n-1) =1    t=1,84  ;     (n-1) =10   t= 1,05 :  (n-1)=100  t=1,005 :    (n-1)=∞    t = 1.   

Como se observa, el estadístico t modifica sensiblemente la Incertidumbre de medición. Cuando se incrementan los grados de libertad como resultado del aumento de observaciones, se reduce el parámetro   t y por lo tanto la Incertidumbre, y viceversa, con la condición:  t  ≥  1.

Por lo tanto la Incertidumbre del tipo ”A”, se evalúa con la siguiente expresión aleatoria: 

Los valores” t” fueron obtenidos de la respectiva tabla la distribución, con una probabilidad normalizada del 68,3% y conforme al particular valor dado a  (n-1).

La Incertidumbre tipo B, u_(B)

Tal lo indicado, las Incertidumbres de este tipo no responden a la modalidad repetitiva de observaciones, pues la técnica de medición se basa en otros métodos conceptuales, tanto para la obtención del Valor medido como para la Incertidumbre
Estas Incertidumbres son evaluadas mediante el juicio científico basado en toda información respecto a la variabilidad de la magnitud sometida a la medición. También es frecuente la asignación de distribuciones probabilísticas arbitrarias generalmente la uniforme o la triangular, conforme a la experiencia que se disponga sobre el procedimiento de medición e instrumental utilizado.
A los fines de unificar la Incertidumbre tipo “B” con respecto a la Incertidumbre tipo ”A” también será considerada como una variable aleatoria y evaluada mediante la definición de la Variancia. El valor particular u(B) dependerá del Mesurando, del tipo de Distribución de la probabilidad arbitraria adoptada y de las condiciones de la medición.
A continuación, se indican las Variancias correspondiente a las siguientes distribuciones:
Uniforme: Variancia = (Límite)2/3
Triangular: variancia = (Límite)2/6
Combinación de las Incertidumbres tipo A y tipo B
Cuando en una medición se presentan Incertidumbres parciales del tipo A y del B con las mismas unidades y en razón que presentan una similitud formal, podrían ser combinadas cuadráticamente , de acuerdo a la Ley de la propagación de las Incertidumbres, (Teorema de las variancias) dando origen a la Incertidumbre compuesta o combinada de la medición, caracterizada por un valor numérico con unidad o bien expresada porcentualmente en % o en ppm.
Incertidumbre Expandida
En determinadas circunstancias, como es el caso de los entes industriales, comerciales, de la salud o reglamentarios, requieren por razones de seguridad una mayor amplitud en el valor de la Incertidumbre. Para ello se dispone del llamado Factor de cobertura, valor numérico >1 vinculado al tipo de Distribución de la probabilidad elegida con valores del (95% o 99%), de acuerdo a lo aconsejado por la experiencia. La Incertidumbre incrementada por dicho Factor suministra la llamada Incertidumbre expandida, de aplicación en los Informes técnicos y en los Certificados de Calibración.

Como elementos de referencia se suministran los Factores de Cobertura para las Incertidumbres tipo A y tipo B